Experiments in a Mark II Economy
Table of Contents
Introduction
Note. The following remarks apply to the experiments as they were originally performed before both spreadsheets were revised. The most important results are described in “The Relation of Energy to Money” and “On EROI and Emergy” hyperlinked to the cover page. The macro controls and cell numbers are incorrect throughout the rest of this file. Don’t do the experiments unless you know the right macro controls. Also, some of the charts may be missing. They are obsolete and will not be needed.
All of the computational experiments performed so far can be carried out on either spreadsheet, namely, http://dematerialism.net/Mark-II-Economy.xls or http://dematerialism.net/Mark-II-Economy-CSP.xls, although many more could have been employed to spare the interested reader the trouble of converging each and every case. But, spreadsheets take up a large amount of web space; so, I have written a number of macros to facilitate changing from one case to another. I would now like to take you through a number of experiments that you can do on this spreadsheet to illustrate the principal features of real political economies provided only that real economies approach the ideals treated here sufficiently closely, e. g., no corruption, etc. When downloading either spreadsheet, you will be asked whether you wish to enable the macros or not. Enable the macros if you plan to perform the experiments suggested by me. If that doesn’t work, lower the security level on the Security menu under the Macros option on the Tools drop-down menu. I now wish to describe the sort of tour I would like you to take:
Download the file http://dematerialism.net/Mark-II-Economy.xls; click the Enable Macros radio button; select the Base Case with <control><shift>A (abbreviated <CS>A). The Base Case (BC) corresponds to an American-style market economy. As we shall see, this type of economy requires the largest energy budget to provide the standard consumption per capita. The percentage saved of the Total Energy Budget, E, relative to the Base Case with the standard settings, the percentage of the total population furloughed relative to the Base Case with the standard settings, and ER/EI* appear in DO28, DO36, and DO43 and in DK39:DM39 for easy tabulation by the experimenter with the Special Paste Value command in the rectangle bounded by DK40 and DM68 (denoted DK40::DM68).
If the number in CV16 is less than about 10-11 and the number in CV17 is less than about 10-12, we have convergence. Otherwise not. If the Base Case is not converged, press <CS>O. This should work unless the spreadsheet is broken, in which case please write me immediately at twayburn@wt.net – if you will be so kind. Then, press <CS>V to set the initial values for GDP, E, and E/GDP for comparison with the results of experiments upon other cases. You are looking at part of the Results Section of the spreadsheet. Let us take the time to notice a few things before we do some experiments.
The principal results are in Column DO. Scroll up until DO18 is visible. This is where the saved value of the GDP for the Base Case with standard variables is stored. If you pressed <CS>A, it should agree with the current value of the Gross Domestic Product, the total of all purchases that have been negotiated by the commerce sector, which includes the purchases made by consumers plus the overhead of the five sectors. The current value of E in DO22 should agree with the saved value in DO35. The change in GDP (DO21) due to an arbitrary investment entered in any one or all of DO31 through DO34, the change in E (DO26) estimated by DO21*DO25, and the change in E (DO27) calculated by the spreadsheet should be zero. (If not, press <CS>V.) Since this is the Base Case, the Percent Saved in DO28 and the Percent Furloughed in DO36 are zero as well.
In Experiment 9 below, I describe a new spreadsheet at http://dematerialism.net/Mark-II-Economy-CSP.xls in which ten equations in the Base Case and sixteen equations in the other cases are solved simultaneously by Newton’s method with the fractions of the population associated with the five sectors held constant. Mark-II-Economy.xls is the spreadsheet on which it is easiest to do experiments as convergence is extremely rapid. When I get a chance, I will go through the early experiments and change the cell identification numbers to whatever is appropriate for Mark-II-Economy-New.xls even though they have not been moved so far from the locations of Mark-II-Economy.xls as to be difficult to find.
On all of the spreadsheets, it is important to change parameters gradually to stay within the domain of convergence of Newton’s method or the various fixed point methods employed. If you are not within the domain of convergence, the computation can diverge and destroy the spreadsheet. That’s why it’s important to save frequently after successes and exit without saving when the computation blows up. For example, suppose you want to reduce the ER/EI as far as you can: Change the factor by which δEE is multiplied by one unit at a time. (δEE is the number of energy units that must be spent by the energy sector to deliver one energy unit to the economy.) Go from 1.0 to 2.0 not 1.0 to 9.0. (This represents a sort of artificial homotopy – just the sort of thing my doctoral thesis was all about. As it turns out, topological degree is invariant under homotopy, which is why a new solution is guaranteed to be found so long as the variables continue to be defined on your computer. See Wayburn, T. L. and J. D. Seader, "Homotopy Continuation Methods for Computer-Aided Process Design," Computers and Chemical Engineering, 11, No.1 (1987).
The Experiments
Experiment 1
For an entire economy, for a median transaction within that economy, or for a transaction of such great scope that such concentrations within particular energy consuming sectors as may exist in one phase or another of the transaction tend to get smoothed out, the energy consumed is approximately equal to the dollar amount of the total cost of the transaction times the Total National Energy Budget (E) over Gross Domestic Product (GDP) ratio (E/GDP) that is tabulated in the DOE database for every country and for every year – within limits. The purchase and operation of a custom-built nuclear power plant is just such a transaction of extremely broad scope to which this type of analysis might apply.
In this study, the product of E/GDP with investments of 1 XD distributed in various ways over the commodities is compared to the actual increase in the total energy budget. The investment is imagined to be made by the energy sector the expenses of which exceed salaries by a small amount. This is compensated for by increases in salaries in the other sectors which are imagined to reimburse the energy sector to account for their fair share of the investment expenses.
In this first exercise, we would like to show that, if an investment is distributed among the commodities in the same proportion as consumer spending is distributed, the increase in the Total Energy Budget, ΔE, will be precisely the increase in the GDP resulting from the investment times (E/GDP)o. The reader should understand that the fraction of the investment that is made in commodity i is mi, which is equal to the cash spent by consumers on commodity i divided by the total cash spent by consumers. The fractions of consumer spending for the four sectors appear in DT31:DT34 where they can be compared to the comparable figures for the US economy in DV31:DV34. (The energy fractions in DX31:DX34, with agriculture, manufacturing, and energy lumped into industrial, can be compared to the figures for the US economy in DY31:34.) The values in DP31:DP34 are these commodity fractions multiplied by 1.0 XD and divided by the price of the ith commodity, which will be cancelled out when that number of units is purchased. Copy the values from DP31:DP34 into DO31:DO34 with the Paste Special Values command and read in DO30 the ratio ΔE computed by the spreadsheet to ΔE estimated by multiplying the change in GDP due to the expenditure of 1.0 XD by (E/GDP)o. If this ratio is 1.0, the experiment has succeeded. Therefore, ΔE/ΔGDP = E/GDP. Don’t forget to zero out DO31:DO34 by copying DR31:DR34 into DO31:DO34 before you do the next experiment.
It is so easy to change from one case to the next that I would do the experiment for all four cases now and then restore the zeroes in DO31:DO34 if there is any reason to doubt the claim. Other distributions or concentrations of the investment cash can be tested in the sequel.
The constant δEE in Cell CF10 is the number of energy units (EU) needed to provide a net energy of 1 EU to the economy. The parameter in DO47 is the factor by which 0.07 is multiplied to get the value of δEE used in the simulation. Clearly, if one wished to compute an ER/EI ratio that considered direct energy requirements only at the first level, the ratio (1 + δEE)/ δEE would suffice. Call that ratio ER/EIo. It corresponds with the ratio computed in many peer-reviewed papers. Nevertheless, I have added an ER/EI routine to the Mark-II-Economy to provide an ER/EI that includes the personal energy requirements of the workers in the energy sector but is also independent of political economy as the workers enjoy the same standard of living in all four political economies considered. I wish to use it to prove a number of points:
1. One can make a distinction between an ER over EI ratio that is independent of political economy and an ER/EI (call it ER/EI*) the EI term of which (EI*) includes the energy costs of the market and of the over-consumption of the higher paid stakeholders in the M, T, and E sectors if they are present and to the extent that they are present.
2. ER/EI ratios that are computed without including the energy costs incurred by the commercial sector in running the market or the energy costs incurred by stakeholders in any of the sectors due to over-consumption lead to optimistic results as far as payback time and feasibility or practicality is concerned. For those who are inclined not to believe this, a logical argument can be found in “On Energy Invested”, which was written earlier to convince people at the Energy Resources Yahoo group.
3. The ER/EI* ratio will improve dramatically as we get rid of a privileged managerial or commissar class or as we get rid of commerce by means of economic planning or, better yet, a give-away (natural) economy.
Let us suppose that we are still in the Base Case (BC). The current value of ER/EI in DO43 has been computed by a special routine in Columns GN through HL. (Press <c>b.) This routine begins with the EUs in FG7 required to provide the total consumption of RUs in DM7. This value appears in GO10 and initializes the standard computation without any direct burden from agriculture, from the direct purchase by consumers of MUs or TUs, or from the purchase of MUs and TUs due to purchasing RUs. The energy costs of the market and of the over-consumption of the higher paid stakeholders in the M, T, and E sectors are included (Switch = 1) or not (Switch = 0) depending upon the switch in DO46. If the over-consumption of managers is included, the effective overheads of MU*, TU*, and EU* in GQ, GS, and GU will be greater than the actual values in GR, GT, and GV. To return to Results Section, press <c>v.
If the switch in DO46 is not 0, set it to zero. The value of ER/EI in DO43 corresponds to the politically independent case. For a δii factor in DO47 of 1.0, the ER/EI is approximately 12.8, which is stored in DO45. Cycle through the cases as before to verify that it is unaffected by political economy insofar as political economy is reflected in the Mark-II-Economy spreadsheet.
Return to the Base Case and set the value of the switch in DO46 to 1.0 to introduce the energy costs of the market and over-consumption costs associated with a US-style political economy. The important thing to notice is that ER/EI* (DO43), which includes the ancillary expenses of commerce and employment, is much lower than the politically independent ER/EI. Tabulate ER/EI* for the Base Case by copying DK39:DM39 into DK41:DM41.
Let us now estimate the factor by which we have underestimated the payback time if we use the ER/EI in DO45. The vender will report the rate, e, at which energy is returned over the lifetime of the device, T. Thus, e = ER/T. Payback time, PT, is the period of time required to generate a quantity of energy equal to EI at the rate e. Therefore, PT = EI/e. Suppose the ER/EI reported by the vender is ε whereas the ER/EI* that determines all of the energy that must be expended to produce 1.0 kW-hour of output is ε*. Then, the actual payback time PT* = EI*/e = ER/(e ε*) whereas the payback time computed from the ER/EI reported by the vendor is PT = ER/(e ε). Since the ER/EI ratios determine the quantity of energy invested per unit of ER and since the technologies will be compared on the basis of equal values of e, we may cancel e and ER to get the payback-time ratio PT*/PT = ε/ε*, the reciprocal of the ratio of the ER/EI ratios, as shown in DO39. This is the factor by which the payback time is underestimated; that is, it will take 3.28 times the period of time to recover the energy invested that one would compute from ER/EI rather than ER/EI*, which would make the vendor’s claim false in the unlikely case that he made such a claim. We now wish to perform this experiment in the other three cases, which will be easy because of the macros:
Press <CS>B to initialize the No-Managers Case (NM). If the NM Case is not converged, press <c>w to set the formulas in DA3, DA4, and DA5 to =CR3, =CR4, and =CR5 then press <c>o repeatedly. Press <CS>V to store the initial values for GDP, E, and E/GDP. Set DO46 to 1, observe the difference between DO43 and DO45, and copy DK39:DM39 into DK42:DM42. The excess consumption of managers is charged to the energy invested; therefore, there is an improvement in ER/EI* from BC to NM. The important difference, though, is in Percent Energy Saved and Percent Furloughed which you have tabulated along with ER/EI* for the NM Case in the table at DK41::DM44 as was done for the BC. Let us repeat this exercise for the No-Commerce Case (NC) (press <CS>C) and No-Commerce-No-Managers Case (NCNM) (press <CS>D), after which the important values for all four cases are available for our inspection in DK41::DM44.
The differences are indeed profound; and, the principal mission of this study has been achieved. Nevertheless, we can do a number of additional experiments of varying interest.
Emergy has been discussed in two or three of my papers as well as in the Wikipedia and Howard Odum’s seminal papers. See, for example, http://tinyurl.com/zsbq6.
Please return to the Base Case by pressing <CS>A and, after setting the formulas in DA3, DA4, and DA5 to =CZ3, =CZ4, and =CZ5 with <c>s, converge the spreadsheet with <c>m (rather than <c>o) to avoid disturbing zM = zT = zE = 1. (In all other cases, after setting the formulas in DA3, DA4, and DA5 to =CR3, =CR4, and =CR5 with <c>w, converge the spreadsheet by pressing <c>o repeatedly.) Press <CS>V. Next, replace the zero in DO31 with 1.0. The value of the change in the total energy budget, ΔE, in DO27 represents the embodied energy (emergy) in one agricultural unit (AU) as this is the amount of energy required to provide one AU by an efficient process in a capitalist-style market economy. Store that value in DJ65 for comparison with the emergies of 1 AU in the other political economies.
Repeat this experiment for 1 RU in DO32, 1 MU in DO33, and 1 TU in DO34 each time making sure that the other cells are zero and leaving them all zero when you are done. (It is not necessary to re-converge the spreadsheet.) Because of the ease with which we can change cases, it makes sense to complete the table of emergies now for all four cases while we are thinking about emergy. (Press <c>w, then <CS>B, then <c>o repeatedly, then <CS>V, then do the experiment; repeat except with <CS>C and <CS>D in place of <CS>B. To restore the Base Case, press <c>s, then <CS>A, then <c>m repeatedly, then <CS>V.)
According to my definition of emergy, it depends upon the political economy, which, after all, impacts the efficiency of the agricultural, manufacturing, transportation, and energy extraction processes as I have gone to great pains to show. However, changes in political economy are, to say the least, rare. Moreover, improvements in agricultural, manufacturing, transportation, and energy extraction processes are infrequent at best and often not implemented after they are discovered. Therefore, emergy is a much more stable measure of value than, for example, money, the purchasing power of which changes with the tide.
In Exercises 4, 5, and 6, I would like to return to the mission discussed in Exercise 1 except that different concentrations or distributions of cash investments in the various commodities will be studied. Let us begin by investing in one commodity at a time.
Return to the Base Case. Set the value in DO31 to 1 AU once again. The ratio of ΔEcalc to ΔEest (= (E/GDP)o · ΔGDP) is again in DO30. Paste its value into DS31. Notice that, for 1AU, the estimated value is too high; but, it has the right order of magnitude. Repeat the exercise for 1 RU, 1 MU, and 1 TU moving down one row each time. Notice that the sum of the products of these values with the fractions in DT31:DT34 will equal one as shown by the final number in DU35. Don’t forget to restore the zeroes in DO31:DO34.
Repeat this exercise for the NM Case, the NC Case, and the NCNM Case all of which should be converged with <c>o (not <c>m) after setting the formulas in DA3, DA4, and DA5 to =CR3, =CR4, and =CR5 with <c>w.
In this exercise, I wish to discover what happens if an investment is distributed among RUs, MUs, and TUs, but not AUs, in the same proportion as they are distributed by consumers in the economy at large. These fractions divided by the relevant commodity price are computed in DZ31:DZ34. The ratio of the ΔEcalc to ΔEest is stored in DZ27. Although the estimate is a little low in the Base Case, the agreement is good. Try the experiment in the other three case. Store the results in DZ28:DZ30. Do not forget to zero out the values in DO31 to DO34 before you change case. And, don’t forget to press <CS>V after you change case. The estimate is low in every case and gets worse as the political economy progresses; however, it is within 11% in all cases and within 6% for a US American-style economy, which is the economy where the technique is most likely to be employed. The inclusion of RUs is appropriate as the installation will require a physical plant.
In “On the Conservation-within-Capitalism Scenario”, using cost data from the Shultz et al. study [http://web.gat.com/pubs-ext/MISCONF03/A24265.pdf], the University of Chicago Study [http://www.nuclear.gov/reports/NuclIndustryStudy.pdf], and the MIT study [http://web.mit.edu/nuclearpower/], I computed an ER/EI ratio of 4.63. See http://tinyurl.com/f8bs7. However, it is not clear that all ancillary costs have been included, e.g., desalination of sea water, remediation of environmental change, etc. A pro-rata share of the costs of providing and maintaining railways to carry heavy equipment, fuel, and waste, highways to transport workers, conduits to transmit electric current, pipelines to transport hydrogen, and easements through which electrical power lines and hydrogen pipelines can be run should be charged to the plant.
Let us see what happens if the investment is distributed over manufacturing and transportation only. The cash fractions divided by price will be computed in DZ41:DZ44 and the results for the four cases in DZ37:DZ40. The results are considerable worse in this case with an estimate nearly 41% high in the No-Commerce Case; however, the agreement is still good enough for my purpose which is to prove a point by a wide margin. An error of 41% or even 100% in my energy calculations for the conservation-within-capitalism scenario would not be sufficient to change the conclusion, namely, that an Apollo project for energy can succeed but not in a market economy.
We wish to demonstrate the unbounded increase in the energy budget and the increased burdensomeness of employment as ER/EI diminishes toward 1.0. We shall not be able to get very close to 1.0 because the number of rows of our spreadsheet required to achieve complete convergence increases beyond my willingness to add rows. I added 408 rows to the spreadsheet for this experiment, but I am not willing to add more. We shall multiply δEE by various δEE factors that we enter in DO47. This amounts to saying that the energy required to deliver 1 EU is greater by the δEE factor.
To begin by changing the value in DO47 from 1.0 to 5.0. Press <c>s to be certain that DA3:DA5 is linked to CZ3:CZ5 as is normally done with the Base Case when changing one of the standard parameters; i. e., DA3 is = CZ3, etc. Then press <CS>A to initialize the Base Case. Press <c>m repeatedly until converged. Press <CS>V. Paste DK39:DM39 into DK47:DM47 and DP51::DS53 into DP55::DS57 for future comparison. Already we notice an increase in total quantity of production required to deliver the same standard of living as ER/EI* decreases.
Since we wish to see if changing to the No-Commerce-No-Manager Case will improve matters, press <c>p to re-initialize the production figures for the M, T, and E sectors so that zM, zT, and zE will reflect constant production per worker as we move from case to case for that δEE factor. Also, change DA3 to =CR3, DA4 to =CR4, and DA5 to =CR5 with <c>w. Then press <CS>D to initialize the No-Commerce-No-Manager Case, and <c>o repeatedly to converge it. Press <CS>V. As before, paste DK39:DM39 into DK48:DM48; but, in the case of DP51::DS53, merely note their close agreement with DK48:DM48 because of the way in which we established zM, zT, and zE. It should be clear how to check the intermediate cases if they are of interest, but I shall continue by increasing the δEE factor in DO47 to 10.0. To see the effect on the δij and fij, press <c>r. To return to the Convergence Section, press <c>a.
It is necessary to do the Base Case first whenever the δEE factor is changed to establish the criterion for setting zM, zT, and zE. Therefore, reset DA3:DA5 with =CZ3, =CZ4, and =CZ5 by pressing <c>s; press <CS>A; and press <c>m repeatedly to convergence. Press <CS>V and paste DK39:DM39 into DK53:DM53 and DP51::DS53 into DP59::DS61 for comparison. The low population of the agricultural sector is disturbing, although it could be argued that everyone is needed to produce energy when the ER/EI gets this low. Press <c>p to re-initialize the production figures.
I looked at the No-Commerce-No-Manager Case again, therefore, I changed DA3:DA4 to = CR3, =CR4, and =CR5 again with <c>w, pressed <CS>D, pressed <c>o repeatedly to convergence, and pressed <CS>V to set Eo GDPo, and (E/GDP)o, and stored my results as before. Finally, I looked at the Base Case and the No-Commerce-No-Managers Case with the δEE factor at 12.0, which is as high as I am willing to go. The results are so impractical as to amount to infeasibility although the ER/EI* is still well above 1.0. Again, the tiny fraction of the population engaged in agriculture is disturbing. I would like to find a way to set πA and let xA float, but I have been unable to do it so far. As soon as xA is floating, variables start going out of bounds from which the algorithm cannot recover. In http://dematerialism.net/Mark-II-BetterCases.xls, I solved this problem by treating the fractions of the population associated with each sector as constants and solving the remaining equations simultaneously. In the Base Case, ten nonlinear equations were solved by Newton’s method; and, in the “better cases”, sixteen nonlinear equations were solved – again simultaneously. The results will be discussed under Experiment 9.
The stored results for Exercise 7 show that as the value of ER/EI decreases monotonically with increases in value of δEE, which is the constant by which the number of energy units delivered (ER - EI) is multiplied to determine the number of energy units required to produce it (EI) at each pass through the economy. As ER/EI approaches 1.0 from above, the total energy budget and total production approaches infinity. Thus, in a modern society the replacement of a high ER/EI primary energy technology by a low ER/EI technology will cause great economic suffering well before it become theoretically infeasible. This experiment was done properly in http://dematerialism.net/Mark-II-BetterCases.xls. The results are graphed in Chart 2, which appears in Experiment 9 below.
Press <c>v. The energy (E), GDP, and E/GDP for that portion of the economy modeled in the dedicated ER/EI computational section is computed and stored in DV45::DX48. Store DV46:DX46 in DV47:DX47 to zero out DV48:DX48. Since there is only one commodity, namely, energy, it should not be surprising that an increase in EX (= ER - EI) of 1 EU would produce a change in the GDP that, when multiplied by (E/GDP)o, gives a value of EI such that (EX + EI)/EI = ER/EI agrees with the ER/EI computed directly. Change the value of DV44 to 1.0 and read the estimated ER/EI in DV43. Compare it to the value of ER/EI in DO43, and don’t forget to change DV44 back to zero.
A new spreadsheet that represents the Mark II Economy solves the problem of keeping the fractions of the population associated with each sector constant regardless of changes in political economy or changes in δEE, the number of energy units required to yield a net energy to the rest of the economy of 1 EU. One EU represents ER – EIo, where EIo is the lowest value of energy invested one might conceivably consider, namely, a value that considers direct energy costs only at the first level and pointedly excludes even the normal energy expenses of the employees of the energy sector. I agree that I am remiss in not discussing ER/EIo = (1 + δEE)/δEE and tabulating it for each of the cases as this is the ratio that gives the highest value of ER/EI. In the new spreadsheet at http://dematerialism.net/Mark-II-BetterCases.xls, I have computed and tabulated the Payback-Time Factor as the payback time required to amortize all of the energy costs that would not have occurred if no energy had been produced divided by the payback time calculated from ER/EIo, the most optimistic payback time. Also, the new spreadsheet has two charts so far. Chart 1 shows the reduction in energy and labor required to produce an invariant standard of living and the increase in ER/EI* as the political economy improves in discrete steps from the unsustainable market economy with two-tier salaries represented by the Base Case (BC) to the No-Managers Case (NM) to the No-Commerce Case with commissars (NC) to the No-Commerce-No-Managers Case (NCNM).
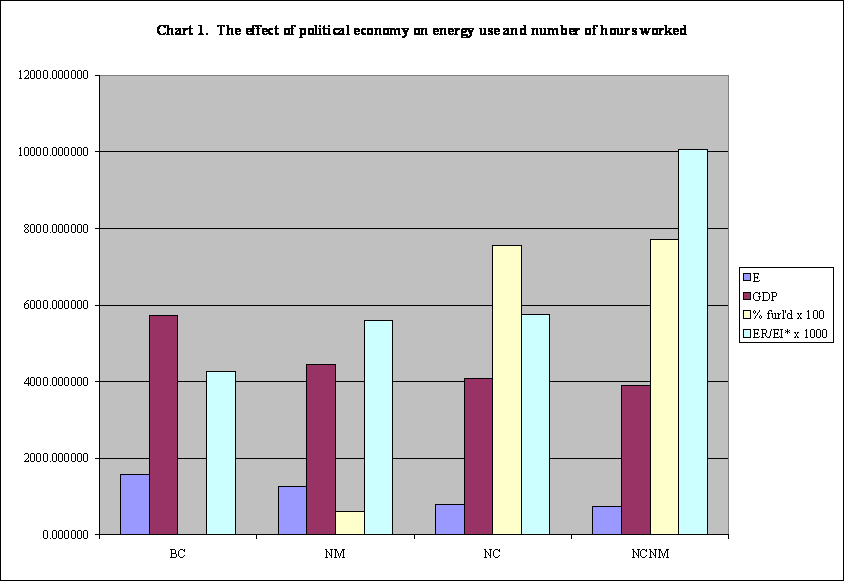
Chart 2 shows the rise toward infinity of the energy budget as ER/EI* diminishes toward 1.0; however, Chart 7 illustrates the phenomenon much better. Therefore, it will be shown next in place of Chart 2, and it will serve for all such experiments to avoid wasteful duplication. Look for other results between columns DC and DZ.
In the earliest versions of the spreadsheet, the fij and the pi were adjusted until the fractions of consumer expenditures, mi, and the fractions of the energy budget, ei, going to the various sectors resembled somewhat the US economy. With a converged solution in hand, it was advisable to fix the ηi and the δij and let the prices, pi, and the fij float as this arrangement corresponds best with physical reality. Indeed, at that time, the problem of matching mi and ei to the US economy by adjusting the fij and the pi seemed insurmountable. However, in http://dematerialism.net/Mark-II-BetterCases.xls, with the simultaneous solution of cash balance equations to obtain the xi and pi, it is easy to match the ei for the Mark II Economy to the ei for the US economy by replacing δiE by (eiUS/miII)δiE, which is done by pressing <CS>Q, solving the cash balance equations, and repeating. With the ei matched, ηi is replaced by (miUS/miII)ηi with <CS>U. A successful sequence of operations is <CS>Q followed by <CS>P once or twice (to solve the cash equations), and repeating until ei match. When the ei match, press <CS>U and <CS>P repeatedly until the mi match. If the ei are no longer matched, repeat entire sequence to convergence. Chart 3 replaces Chart 2 for the new Base Case, which resembles the US economy as closely as it is possible to do with a Mark II Economy; however, Chart 7 above is a better picture. I have not bothered to contrive a method for updating the deltas that does not obliterate the formulas in CF6:CF11; however, the macro executed by pressing <C>t will save the new values of CF6:CF11 in CC6:CC11 and repair the damage.
In an effort to push the economy closer to infeasibility I decided to allow the fractions of the population dedicated to the manufacturing, transportation, and energy sector in http://dematerialism.net/Mark-II-BetterCases.xls to be altered by multiplying them by the values of z in CR3:CR5 and iterating until the production per capita in each of those sectors was what it had been with the original value of δEE. This could be done until the value of δEE reached seven times its original value at which point the population of the commercial sector would have become negative. Therefore, the populations were allowed to remain constant once again and the factor by which δEE was multiplied was pushed all the way to 10.0. The value of ER/EI* indicated in CT380, which is a snapshot of the results, is 1.085; but, this cannot be correct because the negative number in CV362 indicates that EI* is infinite. Thus, at some value of δEE less than 10.0 times the original value of δEE, δEE has passed the point at which ER/EI* is arbitrarily close to 1.0, and ER/EI* is now undefined. The production of MUs, TUs, and EUs had become impossibly high. The economy would have broken down long before this occurred. In any case, I proved to myself that up to a fairly high value of δEE I can retain the original values for production per capita in the manufacturing, transportation, and energy sectors by altering the fractions of the population appropriately.
So far, we have assumed that workers in the commercial sector earn no more than workers in the other sectors. Perhaps, in an American-style economy it might be more reasonable to assume that workers in the commercial sector are principally college graduates; therefore, in this experiment, we have increased their pay by 50% (CV28 = 1.5), which, perhaps, is still conservative. In any case, we wish to find out how much energy and how much labor would be saved by switching to a natural economy with economic equality and no commerce. We assume, as usual, that, in a society where corruption is impossible, the cost of economic planning is negligible. This is a reasonable assumption, but I should say why much earlier in this paper.
In any case, snapshots of the results can be found in the rectangle CP421::DA494 with 65.1% of the energy saved in CT490 and 80.5% of the labor saved in CT491. Indeed, the “elephant in the living room” is the high cost of commerce and the market.
Note. It is important in http://dematerialism.net/Mark-II-BetterCases.xls to restore the value in CV28 to 1.0 before trying to converge any of the “better” cases, that is, better than the Base Case.
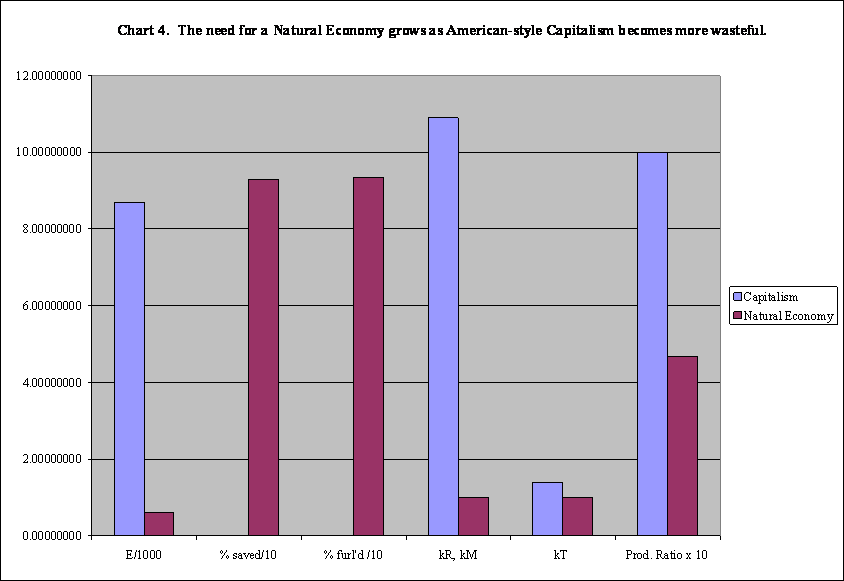
In this experiment, the exercise begun in Experiment 12 is carried out systematically. In http://dematerialism.net/Mark-II-Economy.xls, the value of κ = {1.0, 1.4, 1.4, 1.0) in the Base Case is raised to κ = {1.0, 10.9, 10.9, 1.4}, which amounts to a managerial class that spends 100 times the amount spent by workers on their residences and manufactured goods and five times the amount spent by workers on transportation to account for the super-rich and to account for expensive cars and air travel. In this case, the savings in energy effected by switching to a natural economy amounts to 93%. The complete results are plotted in Chart 4: The need for a Natural Economy grows as American-style Capitalism becomes more wasteful, Chart 1on the spreadsheet.
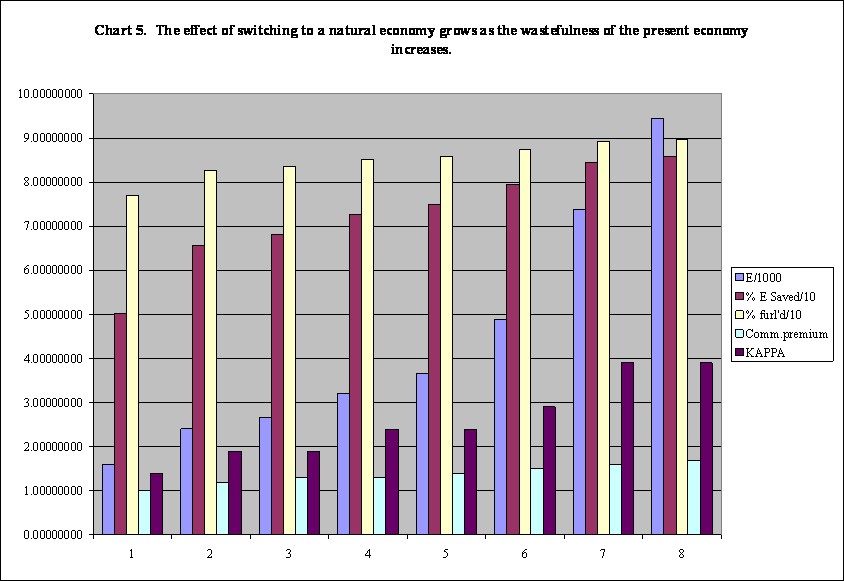
In http://dematerialism.net/Mark-II-BetterCases.xls, due to ease of convergence with Newton’s method it is easy to plot increasing values of the components of κ and the commercial premium mentioned in Experiment 12 until a commercial premium of 1.9 is reached after which the fraction that must be retained to pay salaries in the energy sector exceeds 1.0 and the computation destroys the spreadsheet. One then re-loads the last saved copy. I do not know how to avoid doing this, so I save after each step is completed. Also, I disable the automatic save feature. The complete results are shown in Chart 5, Chart 4 in the spreadsheet. Again, it is important to reset CV28 to 1.0 before trying to converge the No-Commerce-No-Managers Case.
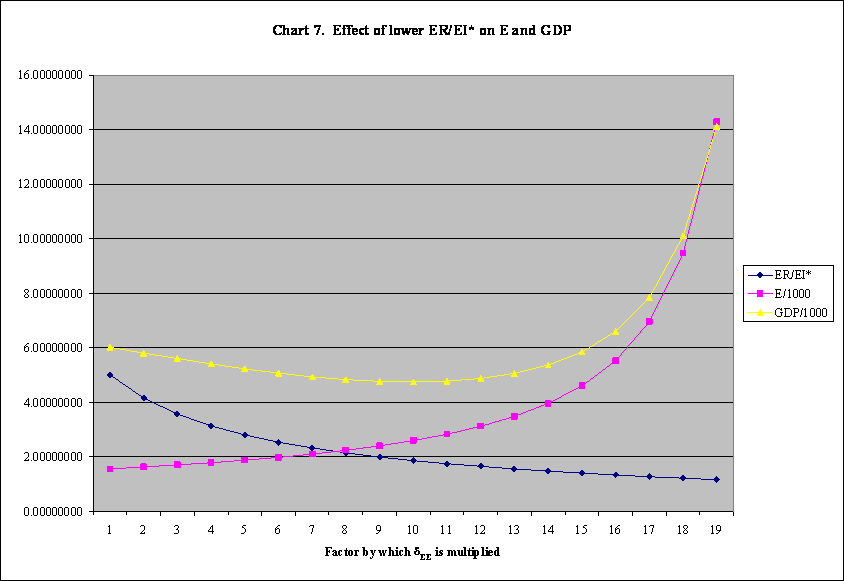
In earlier experiments with lowering ER/EI*, we did not plot the behavior of the GDP, which is affected by the Mark II economic rule that the price of energy remain constant at one X dollar per energy unit. In Chart 5 of in http://dematerialism.net/Mark-II-BetterCases.xls, we were able to increase the factor by which δEE is multiplied all the way to 11.0 and plot E/1000 and GDP/1000 – probably because we are using Newton’s method with analytic derivatives. Regrettably, Chart 5 below shows only the first half of the original version but with smaller step size; therefore, refer to Chart 7 above.
In this experiment on http://dematerialism.net/Mark-II-BetterCases.xls, I reduced the value of δEE to half of its original value when the factor by which it is multiplied is 1.0. Thus, the ER/EIs can be lowered in smaller steps. Chart 7 above is the result.
Rather than try to solve sixteen equations by Newton’s method, I decided to keep the entire population of each sector on active duty and reduce the hours worked per week to take advantage of the savings in overhead in the “better” cases as reflected in the Production ratio in DR50:DR53. The average value in DR54 is shown in CT31, although the production ratios for the sectors should be equal. This has proved more interesting than merely duplicating the results in Mark-II-Economy.xls with faster convergence. Please see http://dematerialism.net/Mark-II-Economy-New.xls. Click Enable Macros; then, when the message “This workbook is linked to other data sources” appears, click Don’t Update. Open up the macros menu on the tools drop-down menu to determine what keys to press to execute the macros or see Table 2 in Appendix A. For one Newton step, press <CS>O. If, in the No-Commerce-No-Managers Case, the production ratio is 0.666, the work day could be reduced from eight hours to five hours and twenty minutes.
According to Figure 8E in http://tinyurl.com/ksk5z, in 2003 the top 10% earns 43% of the income in the United States. Therefore, to simulate American inequality in the Mark II Economy, the managers should earn 6.79 times what the workers earn. Since, in a steady-state economy, everyone spends everything he earns (sic), the expenditures on residential units and manufacturing units must be 1.96 times what they would have been if managers had been paid the same as workers. Also, by iterating on δEE, I have matched an average ER/EIo of 20 for the slate of fossil fuels consumed in the United States.
As ER/EIo is reduced to about 3.0 for the average renewable primary energy technology, we can determine the new energy budget. Assuming a current energy budget of about 100 quads, the energy requirements for ER/EIo = 3.0 will be almost four times Maximum Renewables as determined by Pimentel. On the other hand, if we have shifted to a natural economy, the energy requirements will be less than 92% of Maximum Renewables with one-tenth the number of transportation units and one-half the number of residential and manufacturing units, which is possible since only about 42% of the work force is working and at about half-time too. Indeed, passenger cars and planes will find their proper places in museums, and the era of over-consumption will have ended.
That said, I continued to search the internet until I found a less egregious figure for the percentage of the income earned by the top 10%. According to Table 3.2 in http://tinyurl.com/r4wyr, after taxes and government subsidies, the top 10% earned 31% of the income. Therefore, to be conservative in my claims for the natural economy, I have used this number, which leads to an energy requirement for the steady-state market economy 3.86 times Maximum Renewables and an energy requirement for the natural economy 1.07 times Maximum Renewables computed as before. So, until the population begins to diminish after many of the incentives for excessive procreation are removed, the people will have to avail themselves of a small amount of non-renewable energy or conserve more energy. By reducing the amount of energy required to produce one agricultural unit by 50% (changing the number in CC12 to 0.5), the energy requirement for the natural economy is reduced to 88% of Maximum Renewables. If you do this for the No-Commerce-No-Managers Case, don’t forget to change it back to 1.0.
The latest version of http://dematerialism.net/Mark-II-Economy.xls has two new macros. Try the following:
1. Press <CS>D to set the variables for the natural economy (No-Commerce-No-Managers Case).
2. Press <C>v to change the factors that multiply δiE, i = A, R, M, T, E, C, to account for the huge savings in energy in a natural economy due to extraordinary conservation measures.
3. Press <CS>O repeatedly until the number in CV14 is less than 10-11, which shows that the balance equations are well satisfied.
4. Press <CS>V to set Eo and GDPo.
5. Paste the values in CT32:CT36 into CT191:CT195 using the Paste Special feature of MS Excel if they are not already equal to them.
6. Press <C>a to return to the Convergence Section and notice in CT33 that 75.0% of the base-case energy is saved by switching to a natural economy. The new energy budget is 96.5% of Maximum Renewables as shown in CV39.
7. Press <C>u to restore the base-case values for the factors that multiply δiE, i = A, R, M, T, E, C.
8. Press <CS>A to restore the base-case variables.
9. Press <CS>O repeatedly until the Base Case is converged.
10. Press <CS>V to set Eo and GDPo.
11. Press <C>a to return the cursor to the Convergence Section and to re-format the spreadsheet.
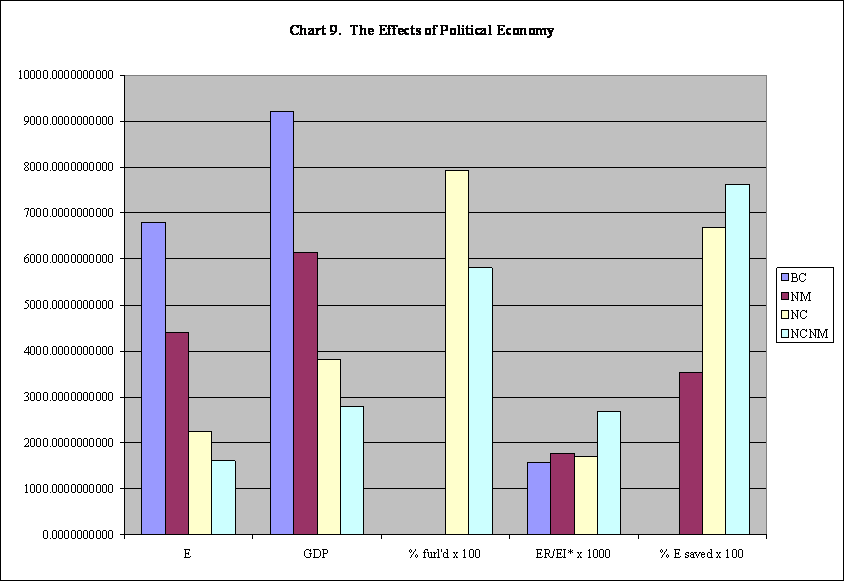
Chart 9 below is a little dated, but it shows the general effects of changing political economy, e. g., substantial reductions of the energy budget.
Additional Experiments
I shall report on additional experiments as I go along.
Summary
Please see http://dematerialism.net/remarks.htm for an introduction to this section. In particular, “Remarks” provides an explanation of the Autonomous Alternative Energy District
In Experiment 4 in which one unit of each of the four commodities is invested one at a time, the change in energy determined by the spreadsheet, ΔEcalc, may be greater or less than the change in energy computed by multiplying one unit by the E/GDP ratio (ΔEest), but it does not vary by as much as a factor of two in these experiments. See DS31:DS34. In Experiment 1 where 1 XD is distributed across the economy, the two quantities are precisely equal. See DO26, DO27, and DO30. This proves that the Energy Invested in ER/EI for the Autonomous Alternative Energy District may be computed by multiplying the monetary costs by the E/GDP ratio.
Very good agreement was found in Experiment 5 for a distribution over the RUs, MUs, and TUs (but not AUs) in the proportion they are distributed over the economy at large; and, in Experiment 6, order of magnitude agreement was found for a distribution over just manufacturing and transportation. Finally, the sum of the products of the calculated energy change over the estimated energy change for the investment of one unit of each commodity separately times the monetary fraction of that commodity’s contribution to total consumer spending is 1.0 exactly if the sum is taken over all four commodities. See DU30:DU35.
In Experiment 2, we demonstrated three important points concerning economic change from (A) an American-style market economy to (B) a Chinese-type communism with markets to (C) a Soviet-style communism with a privileged commissar class to (D) an egalitarian natural economy without markets. In Experiment 3, we tabulated emergy data in a Mark II Economy. Finally, in Experiment 7, we explored what happens if alternative energy technologies with progressively lower ER/EI*s are embraced by all of society.
Undoubtedly, I will continue adding to The Experiments subsequent to the release of this early draft on July 16, 2006. Hopefully, the people who see this will offer useful suggestions, corrections, valuable insights, and, perhaps, solutions to the problems I have left unsolved.
Tables of Macros
|
Table 1. Table of Macros for http://dematerialism.net/Mark-II-Economy.xls |
||
|
BC |
Initialize Base Case |
<CS>A |
|
NM |
Initialize No-Managers Case |
<CS>B |
|
NC |
Initialize No-Commerce Case |
<CS>C |
|
NCNM |
Initialize No-Commerce-No-Managers Case |
<CS>D |
|
Iter A |
Set formulas in DA3:DA5 for Base Case |
<C>s |
|
Iter B |
Set formulas in DA3:DA5 for all other cases |
<C>w |
|
GDPE |
Set GDPo to GDP and Eo to E (to be executed immediately after current case is converged) |
<CS>V |
|
Computation |
Sends cursor to computation section of spreadsheet and auto-fits |
<C>d |
|
EROEI |
Sends cursor to EROEI section of spreadsheet and auto-fits spreadsheet |
<C>b |
|
Show |
Sends cursor to convergence section of spreadsheet and auto-fits |
<C>a |
|
SeeDELS |
Sends cursor to δij section of spreadsheet and auto-fits |
<C>f |
|
Results |
Sends cursor to results section of spreadsheet and auto-fits |
<C>r |
|
PowerM |
Performs several iterations of convergence routine for Base Case |
<C>m |
|
PQX |
Performs one iteration of the convergence routine for the Base Case |
<CS>M |
|
PowerZm |
Performs several iterations of the convergence routine for better cases |
<C>o |
|
Ziter |
Updates the fraction of the M, T, and E sectors on active duty |
<CS>Z |
|
ProdInit |
Sets the initial production for each of the sectors to the current value |
<C>p |
|
Piter |
Updates the prices |
<CS>P |
|
PI |
Updates the fractions of the population associated with each sector |
<CS>Q |
|
Xiter |
Updates the fraction of gross cash retained for salaries for each sector |
<CS>X |
|
Init |
|
|
|
PIConst |
|
|
|
PPI |
|
|
|
RestartBC |
|
|
|
RestartNMNCNCNM |
|
|
|
ToResults |
Sends cursor to results section of spreadsheet and auto-fits |
<C>v |
|
XP |
|
|
|
Table 2. Table of Macros for http://dematerialism.net/Mark-II-Economy-CSP.xls |
||
|
BC |
Initialize Base Case |
<CS>A |
|
NM |
Initialize No-Managers Case |
<CS>B |
|
NC |
Initialize No-Commerce Case |
<CS>C |
|
NCNM |
Initialize No-Commerce-No-Managers Case |
<CS>D |
|
StoreX |
Stores variables in CQ6:CQ26 in CW3:CW26 |
<C>e |
|
RestoresX |
Pastes variables in CW6:CW26 into CQ3:CQ26 (used in finite difference derivatives) |
<C>w |
|
IncrX |
From Sheet 3, pastes values from CZ6:CZ26 into CQ6:CQ26, and ends on Sheet3 with auto-fixed formats (used finite difference derivatives calcs) |
<CS>I |
|
GDPE |
Set GDPo to GDP and Eo to E (to be executed immediately after current case is converged) |
<CS>V |
|
Computation |
Sends cursor to computation section of spreadsheet and auto-fits |
<C>d |
|
EROEI |
Sends cursor to EROEI section of spreadsheet and auto-fits spreadsheet |
<C>b |
|
Show |
Sends cursor to convergence section of spreadsheet and auto-fits |
<C>a |
|
SeeDELS |
Sends cursor to δij section of spreadsheet and auto-fits |
<C>f |
|
NR10 |
Takes one Newton step in Base Case |
<CS>O |
|
TenNR10s |
Executes <CS>O ten times |
<CS>P |
|
NR16 |
Takes one Newton step for better cases |
<CS>Z |
|
TenNR16s |
Executes <CS>Z ten times |
<C>z |
|
UpdateDEL |
Updates δiE to match US energy use data |
<CS>Q |
|
UpdateETA |
Updates ηi to match US consumer purchasing data |
<CS>U |
|
QUP |
Executes <CS>Q, <CS>U, and <CS>P once |
<CS>W |
|
TenW |
Executes <CS>W ten times |
<C>w |
|
FixDELs |
Restores formulas for δiE and their stored values in CC6:CC11 |
<C>t |
|
ProdPerCapInit |
Sets the initial production per capita for each of the sectors to the current value |
<C>q |
|
ProdInit |
Sets the initial production for each of the sectors to the current value |
<C>p |
|
GDPEInit |
Sets Base-Case E and Base-Case GDP to the current values |
<C>r |
|
Low |
Sends the cursor to the finite difference derivatives calculation on Sheet 3 |
<CS>Q |
Thomas L. Wayburn
Houston, Texas
October 4, 2006