Availability Balance on Earth Redux
Helmholtz availability is U – TeS = A and Gibbs availability is H - TeS = B; therefore, the availability balance, which is obtained by multiplying the entropy balance equation by Te and subtracting it from the energy balance equation, is as follows:
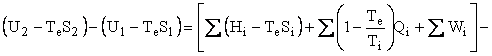
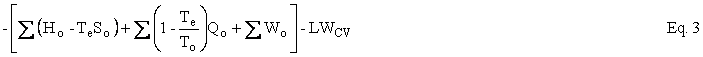
where U is internal energy, H = U + PV is enthalpy, W is work, Q is heat, and T is temperature. The subscripts i, o, and e refer to in, out, and environment.
Earlier work on the availability balance around Earth can be found at http://dematerialism.net/Earth Part 1.html and http://dematerialism.net/Earth Part 2.html.
Let us suppose that, whether the enthalpy H equals the energy U or the enthalpy H = U + PV or whether the enthalpy equals something else, the correct input and output terms to the Earth’s control volume are the enthalpy in and the enthalpy out. Now, the Gibbs free energy of photons and elements is zero; so, Hi = TiSi and Ho = ToSo. For the maximum reversible work for the Earth’s steady-state control volume, Equation 3, for which Hi = Ho = H, reduces to:
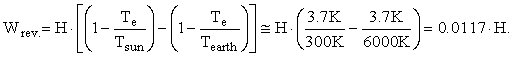
This gives a very large value for the maximum reversible work, but a much smaller value than the value I got before which, in any case, exceeded 100,000 TW. I now get 0.0117 · 1.333 · 127,000 TW = 1984 TW and you get 0.0117 ·127,000 TW = 1488 TW. These are very large amounts of energy, but they are much smaller than 100,000 TW. I have no idea why it took me so long to even look at these numbers although it occurred to me to do this calculation many years ago.
My question to you is: Is this at all correct? What do you think of taking the temperature of deep space as the temperature of Earth’s environment for the purposes of computing reversible work?
Houston, Texas
January 29, 2007
Addendum 10.27.2011 for Energy Resources (Yahoo Group)
Since S = H/T and H = 4/3 E, we have Sin = 4/3 127,000 TW/ 5760K = 29.4 TW and Sout = 666.7 TW/K where S stands for the rate of entropy transfer for simplicity in typing. Thus, Earth receives 637.3 × 109 kilowatt-hour per Kelvin per hour of negentropy from the sun, which overwhelms the entropy production due to the operations of civilization.