Expected Value of Texas Lottery Ticket

Thomas L. Wayburn, PhD

Comments

I do not wish to endorse the notion of lotteries, gambling, and – especially – lotteries run by the State, which putatively looks after the interests of its citizens.  I believe the Texas State Lottery, which amounts to a retrogressive tax on the poor, is immoral, impractical, mean, ugly, and foolish.  It encourages people to want to get something for nothing, to believe that an opulent lifestyle is desirable, and to believe that immoderate consumption by an individual is not harmful to the rest of society.

But, this computation is not based on ethics.  I wish to determine when and when not the Texas State Lottery is a sucker bet, that is, I wish to estimate the expected value.  If the expected value exceeds the price of the ticket we have what gamblers call an overlay, that is, a good bet – you should take it if you’re an avid gambler.  I am assuming that the players share a view concerning taxes not shared by many, namely, that it is a pleasure and a privilege to pay taxes and that paying taxes is just one more indulgence to be enjoyed in a new opulent lifestyle.  Conceivably, the expected value of the ticket may exceed the cost (one dollar) even when payment of taxes at the highest rate is taken into account.  Undoubtedly, these methods can be applied to other state lotteries mutatis mutandis.

Further, I would like to get a lower bound for the expected value and it might be possible to get such a bound by using Stirling’s approximation to the factorial function, but for now I am getting a value that might be slightly too high for two reasons: (i) I am approximating the combination of n things taken k at a time, with n of the order of 50 million and k of the order of six by simply n^k/n!.  I shall indicate the accuracy of this approximation in the text.  (ii) I shall include the tail end of the exponential series.  As we know, exp converges very quickly, therefore, the trailing terms are not large.  But, they do make my estimate slightly high.  This should not be important, though, because the most difficult number to estimate is the number of people who will bet.  This number has been estimated in Austin using fairly sophisticated statistics in order to advertise the size of the Estimated Jackpot for guessing all six number out of fifty, but we shall have to decide for ourselves on the basis of the historical records of the lottery whether the State’s estimates are consistently high, low, or indifferent.  The error in our guess of the number of one-dollar tickets sold, N, should make the other approximations in our formula of little or no significance.

Finally, my only motivation for this exercise, other than the pure pleasure of doing elementary mathematics as an amateur, is to determine when, if ever, the Texas State Lottery is not a sucker bet.  This exercise was inspired by A. K. Dewdney’s book 200% of Nothing, John Wiley, New York (1993), which was to be used in “ambassador” programs in the public schools to stimulate interest in mathematics and science among young people.  This seemed like a topic to which many “at-risk” children might be able to relate.  Moreover, it might not be prohibitively expensive to print up lottery-ticket size fliers that explain expected value on one side and our estimate of the expected value of the forthcoming drawing on the other.  These might be distributed outside lottery ticket outlets – primarily convenience stores, which, by the way, are always complaining about getting robbed.

The rules for cash distributions will be given in some detail in the section on estimating the number of players.  Suffice it to say for now that 32% of the gross receipts, i.e., the Grand Prize or jackpot is divided equally among the tickets showing the six correct numbers.  If no one chooses all six numbers, the 32% of the gross sales is rolled over and added to the six-number jackpot, but not as an interest bearing amount.  This is continued until one or more people split the Grand Prize.  The Grand Prizes are paid out over 19 years in 20 installments: the first immediately, the remaining at one-year intervals.  What is not paid immediately is deposited in conservative bonds of the manager’s choosing on Thursday morning after the Wednesday drawing and on Monday morning after the Saturday drawings.

We should discuss some subtleties due to the payment of exactly $3.00 for choosing 3 out of 6 and due to the minimum of the Grand Prize having been arbitrarily set at two million dollars.  I don’t know if this minimum includes the time-value of money or not.  Those tickets that have correctly selected 5 out of 6 numbers divide up 2.5% of the total cash intake, i.e., the number of one-dollar tickets sold.  The choosers of 4 out of 6 divide up 9%, and, as mentioned above, the choosers of 3 out of 6 get precisely $3.00.  One percent of the gross sales is set aside in a fund to account for the possibility that the sum of the three-dollar prizes exceed the estimated 5.5% set aside for this distribution.  It must be noted that the State takes 50% of the gross sales off the top for its own purposes, primarily education – if one may call what is imparted in the schools education.

Contribution to Expected Value of Choosing Six Out of Fifty

We must first calculate the probability of drawing the correct six numbers out of 50 regardless of order.  Since the probability is the number of  favorable outcomes divided by the total number of equally expected possible outcomes, the probability of drawing 6 out of 50 is p_o = the reciprocal of the combination of fifty things taken six at a time – which last is written 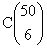 .  Thus,

 

The probability, q_o, that we do not win, then, is 1- p_o =   .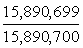

That was easy.  We must next calculate the expected value of winning the big prize.  Let  p₁ be the probability that we win and everyone else loses, that is, we are the sole winner.  Suppose there are N tickets sold and we buy the N+1th ticket.  (The tickets are one dollar each, so the cash intake in dollars is the number of tickets sold.)  Let  be the probability that our ticket is the sole ticket that picks all six numbers correctly.  (The back-superscript refers to N+1 tickets; the forward superscript N refers to exponentiation.)  Similarly, the probability that our ticket is one of two winning tickets is

 

since any of the other N tickets might be the second winner.  Likewise,

 _,

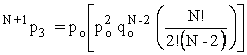since any two of the remaining tickets might be the second and third winners.  Continuing on in this vein:

                                          ·

                                          ·

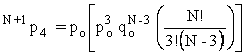
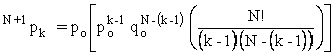
Provided we neglect the possibility of picking 5 out of 6, 4 out of 6, and 3 out of 6, the expected value of a one dollar ticket is

 _,

where R_m is the accumulated amount from jackpots not won in consecutive drawings.  The terms rise at first then slowly decrease.  The probability of 100 winning tickets (when N = 50 million) is so small that the final terms in the series, which contains 50,000,001 terms must contribute very little to E.  Computations have not been made for more than five winners.  Historically, the number of winners has rarely exceeded five, which occurred on 3-16-94.  Undoubtedly, it is safe to assume our approxi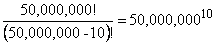mation  is good.  Calculations have been made for the approximation

 _.

 In case N = 50,000,000 and k = 5, let’s look at the terms of

  

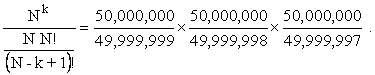
The last term is the largest and equals only 1.0000006.  Since there are three terms the error is less than 1.00000006³ = 1.00000018.  This is not likely to influence our bet and the more elegant calculation with Stirling’s Formula to get a true lower bound can be postponed or rejected out of hand as not worth doing.

Let’s suppose, for the time being, that we know the number of tickets, N, that will be sold (other than our ticket) and the exact grand prize, W.  We compute the contribution of the probability of winning the grand prize to the expected value of a lottery ticket as follows:

since k (k-1)! = k!.  So,

                               

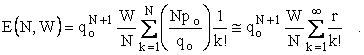
Thus, since

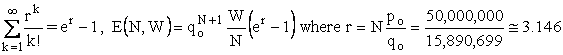
for N = 50,000,000.  For  r = 3.146, we get the following table of k, k!, and r^k/k! :

 

 

One can imagine what this table would look like if it went up to fifty million.  Note that

  

The terms in the exponential series after the fifty millionth term contribute virtually nothing and can safely be neglected – even though they too make our number slightly too large.

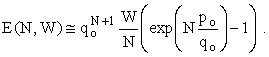
Suppose W = $50,000,000 (50 MB) and N = 50,000,000 (50M).  Then, the sum of the first ten terms is 22.246,

 

and E(N,W) = 0.043 × 22.246 =  $0.957 .  So, until we add the contribution from picking 5, 4, or 3 numbers we can’t bet.  (Actually, the above calculation is completely unrealistic because of the annuity factor.  This is another example of questionable ethics on the part of the State.  The Estimated Jackpot published in the press has been multiplied by an annuity factor, which I compute to be about 1.74.  This is to account for the fact that the Grand Prize is to be distributed in 20 equal installments over essentially nineteen years.  The interest that will be earned by the last nineteen installments is taken into account; but, since this money doesn’t really exist at the time of the drawing, I cannot take credit for the time-value of the actual prize in my computation.  If 50,000,000 one-dollar tickets are sold, the contribution to the prize is only 16MB (megabucks).  It is highly unlikely that the rollover would have been as great as 34MB.  In fact, we can divide by 1.74 to find the actual prize, namely, 28.736MB, which indicates that the rollover was only about 12MB.  Thus, my early computations were far too optimistic because I did not know about the annuity factor.  The case of W = 50MB and N = 50M (million) never happens.  It may turn out that, in every instance so far, the ticket has been, without exception – a sucker bet, i.e., the expected value was below one dollar.  Naturally, unless the pot is very large and the market for ticket sales is saturated, it will always be a sucker bet.  Nevertheless, I shall suggest a hypothetical situation in which it is not a sucker bet.

Contributions from More Likely Events

We must next adjust our formula to account for the fact that we may hit 5, 4, or 3 numbers, which will increase E(N,W).  Then we must try to calculate N from the State’s well-publicized Estimated Jackpot.  We have historical data from Austin that will permit us to determine how good the State’s prediction is.  We can calculate the annuity factor that the State is using.  Since it varies only slightly, we can use a value that approximately minimizes the difference between the calculated prize and the published prize.  This can be done by trial and error on a spreadsheet.  Finally, we will merely state Stirling’s Formula and leave it to the young and the restless to employ it to get a genuine lower bound.  Unfortunately, the best lower bound one gets may be far too conservative to be useful.

Let r be the probability of picking 5 out of 6 numbers, s the probability of not doing so, t the probability of picking 4 out of 6 numbers, u the probability of not doing so, v the probability of picking 3 out of 6 numbers, and w the probability of not picking 3 out of 6.  Let p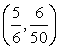 be the probability of picking 5 out of 6 once the six winning numbers have been chosen.  Then,

 

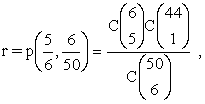
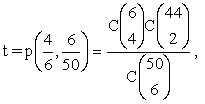
and, finally,

 

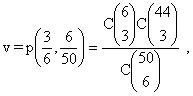
where the subscript (zero) has been suppressed.

These are readily evaluated.

We can now write, by analogy, the formulas for  , the probability of being the only person who picks 5 out of 6 and so on:

 

                              _·

                              _·

                              _·

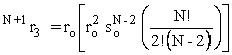
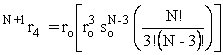
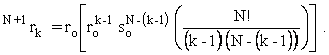
Likewise for 4 out of 6.  The contribution to the expected value from the possibility of guessing three numbers correctly is much simpler because the prize is $3.00 regardless of the number of winners.

We may now observe that when no one wins the Grand Prize, it is “rolled over” (without interest) and added to the ensuing Grand Prize along with 32% of the gross for that drawing.  Let us call 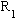 the rollover for the first drawing with no Grand-Prize winner, 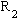 for the second, etc.  If the Grand Prize is won on the mth drawing (since the last award of a Grand Prize), the total amount rolled over is 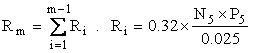 is the value of the rollover for the ith drawing where N₅ is the number of 5-number winners and P₅ is the prize received by each.  Both of these numbers are published in the newspaper and, since the amount is paid immediately, there is no annuity factor.  It is up to the player to keep a running total of the rollovers from this information.  The contribution to the expected value of the possibility of winning the Grand Prize, then, is E⁽⁶⁾(N) since W₆ = 0.32N + R_{m .}  Similarly, W₅ = 0.025N, W₄ = 0.09N, and W₃ = 3 dollars.  Thus E is a function of N alone and not both N and W.

 

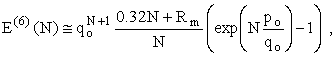
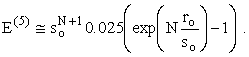
Unfortunately, the approximation 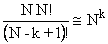 will not do for E⁽⁴⁾.  The number of winners, k, is way too large.  We must retreat to the more primitive equations from which the above equations were derived.  In fact, a good number to use for an upper bound on the number of tickets with four correct numbers is 60,000.  Thus,

 

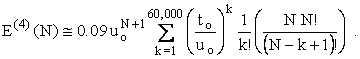
The total expected value is E(N) = E⁽⁶⁾ + E⁽⁵⁾ + E⁽⁴⁾ + E⁽³⁾.  Whereas E⁽³⁾(N) is just $3.00, v_o, the expression for E⁽⁴⁾(N) is extremely intractable numerically because of the large exponents and factorials.  Perhaps a symbolic processor is indicated.  (Note. One might be able to evaluate it by hand by choosing the order of the factors judiciously, always multiplying by something small immediately after multiplying by something large.  This would take some difficult FORTRAN programming using MAX and MIN liberally.  I have worked out an algorithm, but the coding would not be simple.)  We can get at the values of E⁽⁵⁾(N) and E⁽⁴⁾(N) another way though.  The contribution to the expected value of E⁽⁵⁾(N) is roughly

  

Of course, the a priori probability that N₅ tickets will have five correct numbers is not N₅/N, but the approximation 0.025 is corroborated below by our calculation using the correct formula.  Similarly, 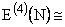 0.09.  The calculation 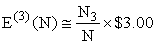, which we can estimate using our tables of statistical data, agrees almost exactly with the correct value as the sample size is very large.

Thus, we are done (except for numerical problems) if we can estimate the value of N from the highly publicized Estimated Jackpot.  I expect E⁽⁴⁾(N) to contribute $0.09 just as E⁽⁵⁾(N) contributes $0.025. E⁽³⁾(N) contributes just about a nickel, i.e., $0.05.  Thus, the final working formula for the Expected Value of a Texas State Lottery Ticket is

 

where

 

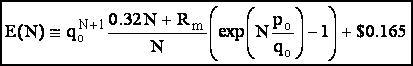
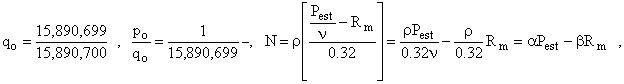
and

The calculation of N using these equations is discussed below.

Estimate of Actual Number of Tickets Sold from the State’s Published Value of the “Estimated Jackpot”

For this we have employed a spread sheet.  We are provided with the historical results of the Texas State Lottery from 11-14-92 to 4-2-94.  This includes, for each date on which there was a drawing, the winning numbers, the estimated jackpot, the number of winners, the annuitized prizes for picking all six (the Grand Prizes), the number of tickets that picked five out of six, the associated prize per ticket, the corresponding data for four out of six, and the number of tickets that won $3.00.  Some of the figures are inconsistent with the formulas, and there are some flat out mistakes, but the data is good enough to check the accuracy of the guesses made concerning how many tickets will be sold for the large jackpots.  We can determine the actual number of tickets sold by multiplying the number of 5-out-of-6 winners by the 5-out-of-6 prize and dividing the result by 0.025.  This number always is an integer, which is encouraging.  The expected number of tickets sold can be back-calculated from the formula

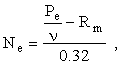
where P_e is the estimated jackpot (widely publicized), n is the annuity factor, used by the operators of the lottery to account for the fact that the jackpot will be paid in 20 equal yearly portions, nineteen of which have been invested in high-grade fixed-interest bearing bonds, 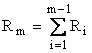, R_i is the rolled-over amount corresponding to what the jackpot would have been had someone picked all six numbers, and m is the number of the drawing since the last grand prize was won.  I calculated an average annuity factor from the actual data.

I found the average value of the ratio of actual to expected numbers of tickets sold to be about 1.1 for the data we examined, which was not the entire set.  The standard deviation was 0.169.  If my understanding of statistics is at all in the right ballpark, this means that estimating the number of tickets to be sold by multiplying the State’s estimate (as calculated from the Estimated Jackpot) by 1.1 is not very precise.  Nevertheless, that is what we shall do for one of the larger jackpots of the past in the following trial calculation.

Trial Calculation

As an example of our method, and to explore the effect of multiplying the number of tickets estimated by the State by 1.1, we shall perform the following calculations on the jackpot of 3-16-94 of 77.110MB (megabucks):  The total expected value, then, is

 

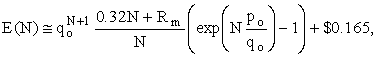
with

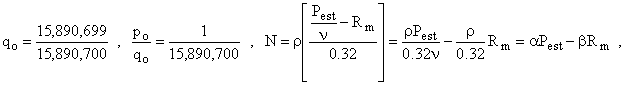
and

 

On 3-16-94, the Estimated Jackpot was 75MB and the total rollover (available from information in the newspaper about how manadditional discussion of ambassador programs any 5-number winners there were in previous drawings and their prizes) was 28.093MB.  Thus, we should use a value of N equal to 51.616M.

It is easy to compute that the contribution to the expected value from the possibility of hitting all six numbers, E⁽⁶⁾(N), is $0.83.  The contribution to the expected value from the possibility of hitting five out of six numbers, E⁽⁵⁾(N), requires some tricky numerics, which I leave as a calculator exercise for the reader, but the upshot is that it contributes only about $0.025.  We use the empirical probability, discussed above for E⁽⁴⁾(N), namely, $0.09, and the correct value of $0.05 for E⁽³(N) to get a final sum of $0.995 for a reasonable upper bound on the expected value of the Texas State Lottery on March 16, 1994.  On this basis, it is a toss-up to decide whether or not this is a sucker bet.  (This is not a great bet, but no worse than what you would get at Las Vegas or at the racetrack.)

Suppose, for a moment that we took the State at its word and used a value of r = 1.  This would have raised the expected value from $0.995 to $1.047.  Thus, the under-estimation of N encourages the gambler to bet.  In fact, the actual number of tickets sold was 51.942M (higher than our estimate of 51.616M); so, as gamblers, we would have been suckered.

It is interesting to note, however, that if no one had won the Grand Prize on 3-16-94 and the ticket market were saturated at 50M, then the expected value would have been $1.327 at the next drawing and we would indeed have an overlay, i.e., a bet that is not a sucker bet.  As far as I know this has never happened and every bet so far has been a sucker bet – as suggested by A. K. Dewdney in his book 200% of Nothing, John Wiley, New York (1993).

Stirling’s Formula

For those readers who wish to try for a true lower bound on the expected value of a Texas lottery ticket I have included gratuitously Stirling’s Formula.  For large values of N:

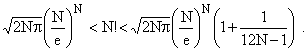
Also,

 

which is true for the log to any base.  Don’t forget to enjoy the exercise because “math in earnest should be fun and math for fun should be in earnest”.

Houston, Texas

September 21, 1994

Revised for submission to the American Mathematical Monthly July 28, 1995

Revised August 1, 1997